I started writing the previous post several weeks ago, and, of course, the ideas are not original with me, in fact, a whole recent issue of “The American Statistician” is dedicated to not just trying to eliminate talk of statistical “significance”, but to provide alternatives.

One of the problems is illustrated by this figure from an editorial in “Nature” which discusses that journal issue: (Amrhein V, et al. Scientists rise up against statistical significance. Nature. 2019;567(7748):305-7) The figure showing real life data from 2 studies:

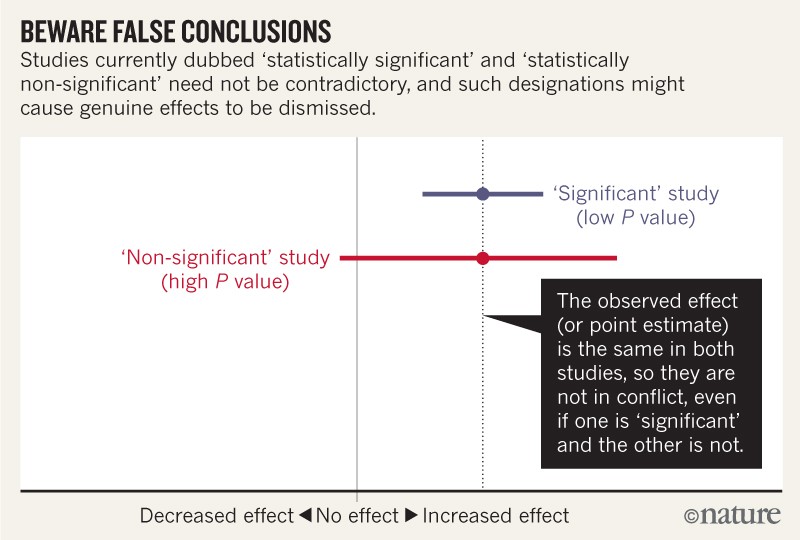
For example, consider a series of analyses of unintended effects of anti-inflammatory drugs. Because their results were statistically non-significant, one set of researchers concluded that exposure to the drugs was “not associated” with new-onset atrial fibrillation…. and that the results stood in contrast to those from an earlier study with a statistically significant outcome.

Now, let’s look at the actual data. The researchers describing their statistically non-significant results found a risk ratio of 1.2 (that is, a 20% greater risk in exposed patients relative to unexposed ones). They also found a 95% confidence interval that spanned everything from a trifling risk decrease of 3% to a considerable risk increase of 48% (P = 0.091; our calculation). The researchers from the earlier, statistically significant, study found the exact same risk ratio of 1.2. That study was simply more precise, with an interval spanning from 9% to 33% greater risk (P = 0.0003; our calculation).

It is ludicrous to conclude that the statistically non-significant results showed “no association”, when the interval estimate included serious risk increases; it is equally absurd to claim these results were in contrast with the earlier results showing an identical observed effect.

Similar things happen all the time in our field, where results with wide confidence intervals which cross a relative risk of 1 are reported as showing “no effect” or “no statistically significant effect”.

Here is a real neonatal example, the classic interpretation of the Davidson study would be that inhaled NO does not prevent ECMO in term babies with hypoxic respiratory failure, as the 95% confidence intervals for their RR of 0.64 include 1.0. The classic interpretation of the other two studies is that inhaled NO does prevent ECMO, but one, NINOS, had a relative risk that was actually less extreme than Davidson, at 0.71, but the confidence intervals don’t include 1. In reality all 3 studies show about the same effect, two being more precise than the third. In some (most) journals you would have to state the results in that way, and would not be allowed, when reporting the Davidson trial, to note the fact that ECMO was less frequent after iNO (although clearly it was), because it is not “statistically significant”.

I think we have to be ready to embrace uncertainty, to realize that dichotomizing our research into reports of things that work and things that don’t work, is unhelpful and may retard clinical advances.

The whole issue of ‘The American Statistician” is devoted to “moving to a world beyond p<0.05” and the opening editorial is well worth the read (Wasserstein RL, et al. Moving to a World Beyond “p < 0.05”. The American Statistician. 2019;73(sup1):1-19). One of the major themes is to stop saying “statistically significant” as a term,  as the distinction between the statistical and the ordinary world meaning of “significant” is now hopelessly lost. 

no p-value can reveal the plausibility, presence, truth, or importance of an association or effect. Therefore, a label of statistical significance does not mean or imply that an association or effect is highly probable, real, true, or important. Nor does a label of statistical nonsignificance lead to the association or effect being improbable, absent, false, or unimportant. Yet the dichotomization into “significant” and “not significant” is taken as an imprimatur of authority on these characteristics. In a world without bright lines, on the other hand, it becomes untenable to assert dramatic differences in interpretation from inconsequential differences in estimates. As Gelman and Stern famously observed, the difference between “significant” and “not significant” is not itself statistically significant.

So what should we do? There are useful suggestions at the end of that editorial, and the authors of each paper were asked to come up with positive suggestions, rather than just a list of “don’t”s.

Overall the suggestions are given the mnemonic “ATOM” Accept uncertainty, be Thoughtful, Open and Modest.

One specific suggestion is that we might continue to report P-values, but as exact continuous values, (p = 0.08, or 0.46) without any threshold implications by the use of < or > notation. I think that could be useful as a way to eliminate the tyranny of p<0.05. It could reduce the risk of “p-hacking”, which is the tweaking of analysis, or even of data, in the search for a p-value which is just under 0.05. They further suggest that such exact p-values should be accompanied by other ways to present the results, such as s-values, Second generation p-values (SGPV), or the false positive risk, all of which they explain, and all of which themselves carry difficulties or unknowns.

Another suggestion is to refer to what are now called confidence intervals as “compatibility intervals”, the idea being that you would state that your result is most compatible with a range of effect sizes between Y and Z, rather than concluding that if the 95% confidence interval includes 1 the difference is not real, but, if it just excludes 1, then there is a real difference between the results. (That would be no better than relying on p<0.05).

The nexus of openness and modesty is to report everything while at the same time not concluding anything from a single study with unwarranted certainty. Because of the strong desire to inform and be informed, there is a relentless demand to state results with certainty. Again, accept uncertainty and embrace variation in associations and effects, because they are always there, like it or not. Understand that expressions of uncertainty are themselves uncertain. Accept that one study is rarely definitive, so encourage, sponsor, conduct, and publish replication studies. Then, use meta-analysis, evidence reviews, and Bayesian methods to synthesize evidence across studies.

I would recommend anyone involved in designing and analysing research to read the editorial and the article which immediately follows it (Ioannidis JPA. What Have We (Not) Learnt from Millions of Scientific Papers with P Values? The American Statistician. 2019;73(sup1):20-5) which is a review of many studies that John Ioannidis has published which show the insidious impacts of the term “statistical significance” and the focus on testing for p-values below a threshold.

One unexpected benefit of eliminating the words “significant” and “significantly” as well as their opposites would be a reduction in the number of words in a manuscript, which could be used for other things. In the recent publication from the Stop-BPD trial that I posted about recently, the words significant and significantly were used 19 times.

In contrast, I am currently revising an article for publication, and it is actually quite difficult! It is so ingrained to think of p<0.05 being significant that trying to come up with other ways of talking about the results of statistical tests can require some actual thought about the meaning of your results!

More seriously, the tyranny of p<0.05 and the use of the words “significant” and “non-significant” lead to a distortion of the English language. For example, a study with 100 patients per group might find that one group has a mortality of 10% and the other has a mortality of 20% (p=0.075,), it would be dangerous and misleading to state “there was no difference in mortality” just because the p-value was too large “p>0.05”, or “NS”.

This is also not a “trend”, a word which implies that things are moving in that direction, it is a real finding in the results, but like all real findings it can only give an estimate of what the actual difference would be if the 2 treatments were given to the entire population. That actual difference is unknowable, and we should be more careful about pretending we know what the actual difference is. Any result from a trial is only an estimate of the true impact of the intervention being tested, an estimate which gets closer to the likely probable true impact as the compatibility intervals become smaller, as long as there are no biases in the trial.

It is also, I think wrong to suggest that the difference is “non-significant” only because of lack of numbers. That always presupposes that a larger trial would have found the same proportional difference (100/1000, vs 200/1000), and that it would then become significant (p<0.001, sorry about the < sign, but the software doesn’t give actual p-values when they are that small!) In reality a larger study might show a mortality difference anywhere within, or beyond, the compatibility intervals of the initial trial.

A better way of presenting those data would be the actual continuous p-value from Yates corrected chi-square, which is 0.075, the actual risk difference in deaths, 0.2 – 0.1, that is, 0.1 and the 95% compatibility intervals of that difference which are 0.07 to +0.26. So the sentence in the results should read something like, “there was a 10% absolute difference in mortality between groups 10% vs 20%, p=0.075, a difference which is most compatible with a range of impacts on mortality between a 7% increase and a 26% decrease”. That is longer than saying “no difference in mortality”, but it has the advantage of being true, and of using some of the words you saved by eliminating “significant” from the paper. It also alerts readers and future researchers that there is a potential for substantial differences in a major clinically important outcome, which does not happen when the terms non-significant, NS, p>0.05, or no impact, are used.

I am going to do my best to avoid thinking of statistical tests as yes or no, true/not true, effective/not effective, and to avoid the word “significant” in my publications, I wonder how long until an editor tells me that doesn’t work, and I have to say it, or makes me say “no difference” because p>0.05.